某公司拟选择一些股票进行证券组合投资,目前选定了甲、乙、丙三只股票,三只股票在不同经济状况下的投资收益率及其概率如表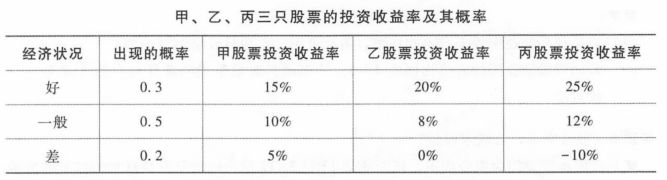 所示。
所示。
要求:
(1)分别计算甲、乙、丙三只股票的预期收益率。
(2) 分别计算甲、乙、丙三只股票预期收益率的标准差(用百分号表示)。
(3) 分别计算甲、乙、丙三只股票预期收益率的标准差率(用百分号表示)。
(4)该公司打算选择三只股票中风险相对较低的两只股票进行组合投资,请问应该选择哪两只股票,为什么?
(5)根据(4)的结果,如果选择的两只股票的投资比重各占50%,计算该组合的预期收益率。
(6)根据(4)的结果,如果选择的两只股票的投资比重各占50%,假设这两只股票的相关系数为0.2,计算该组合收益率的标准差。
(7)根据(5)的结果,如果选择的两只股票的投资比重各占50%,假定资本资产定价模型成立,该组合的预期收益率和投资者的必要收益率相等,证券市场平均收益率是12%,无风险利率是5%,计算组合的β系数。
(8) 该公司又关注到市场上丁公司股票,想要进行投资。已知丁公司股票当前的市场价格为13元/股,丁公司采用固定股利政策,每年的股利固定为2元/股,丁公司股票的β系数为1.2,证券市场平均收益率为12%,无风险利率为5%,判断丁公司股票是否值得投资。
 所示。
所示。要求:
(1)分别计算甲、乙、丙三只股票的预期收益率。
(2) 分别计算甲、乙、丙三只股票预期收益率的标准差(用百分号表示)。
(3) 分别计算甲、乙、丙三只股票预期收益率的标准差率(用百分号表示)。
(4)该公司打算选择三只股票中风险相对较低的两只股票进行组合投资,请问应该选择哪两只股票,为什么?
(5)根据(4)的结果,如果选择的两只股票的投资比重各占50%,计算该组合的预期收益率。
(6)根据(4)的结果,如果选择的两只股票的投资比重各占50%,假设这两只股票的相关系数为0.2,计算该组合收益率的标准差。
(7)根据(5)的结果,如果选择的两只股票的投资比重各占50%,假定资本资产定价模型成立,该组合的预期收益率和投资者的必要收益率相等,证券市场平均收益率是12%,无风险利率是5%,计算组合的β系数。
(8) 该公司又关注到市场上丁公司股票,想要进行投资。已知丁公司股票当前的市场价格为13元/股,丁公司采用固定股利政策,每年的股利固定为2元/股,丁公司股票的β系数为1.2,证券市场平均收益率为12%,无风险利率为5%,判断丁公司股票是否值得投资。
正确答案:
(1)甲股票的预期收益率=0.3×15%+0.5×10%+0.2×5%= 10.5%
乙股票的预期收益率=0.3×20%+0.5×8%+0.2×0=10%
丙股票的预期收益率= 0.3×25%+0.5×12%+0.2×(-10%) = 11.5%
(2)
(3)甲股票预期收益率的标准差率=3.5%/10.5% =33.33%
乙股票预期收益率的标准差率=7.21%/10%=72.1%
丙股票预期收益率的标准差率= 12.13%/11.5% = 105.48%
(4)选择甲股票和乙股票。因为预期收益率不同时,标准差率小的股票风险小,所以该公司应当选择甲股票和乙股票进行投资组合。
(5)组合的预期收益率=10.5%×50%+10%×50%=10.25%
(6)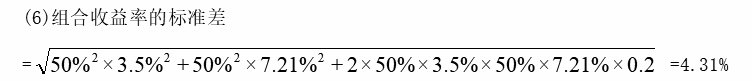
(7) 方法一:根据资本资产定价模型: 10.25%=5%+β×(12%-5%), 解得:β=0.75,即组合的β系数为0.75。
方法二: 10.5%=5%+β甲×(12%-5%), 解得: β甲=0.7857;
10%=5%+β乙×(12%-5%), 解得:β乙=0.7143。
组合的β系数= 0.5×0.7857+0.5×0.7143=0.75
(8) 购买丁公司股票的必要收益率=5%+1.2×(12%-5%) = 13.4%
丁公司股票的价值=2/13.4%=14.93 (元/股)
丁公司股票价格13元/股小于其价值14.93元/股,丁公司股票值得投资。
乙股票的预期收益率=0.3×20%+0.5×8%+0.2×0=10%
丙股票的预期收益率= 0.3×25%+0.5×12%+0.2×(-10%) = 11.5%
(2)

(3)甲股票预期收益率的标准差率=3.5%/10.5% =33.33%
乙股票预期收益率的标准差率=7.21%/10%=72.1%
丙股票预期收益率的标准差率= 12.13%/11.5% = 105.48%
(4)选择甲股票和乙股票。因为预期收益率不同时,标准差率小的股票风险小,所以该公司应当选择甲股票和乙股票进行投资组合。
(5)组合的预期收益率=10.5%×50%+10%×50%=10.25%
(6)
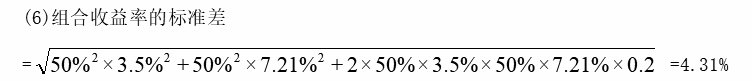
(7) 方法一:根据资本资产定价模型: 10.25%=5%+β×(12%-5%), 解得:β=0.75,即组合的β系数为0.75。
方法二: 10.5%=5%+β甲×(12%-5%), 解得: β甲=0.7857;
10%=5%+β乙×(12%-5%), 解得:β乙=0.7143。
组合的β系数= 0.5×0.7857+0.5×0.7143=0.75
(8) 购买丁公司股票的必要收益率=5%+1.2×(12%-5%) = 13.4%
丁公司股票的价值=2/13.4%=14.93 (元/股)
丁公司股票价格13元/股小于其价值14.93元/股,丁公司股票值得投资。

